Selten habe ich so lange an einem Rätsel getüfftelt. Schlußendlich hab ichs trotzdem nicht rausgefunden.
Wie kann das sein????
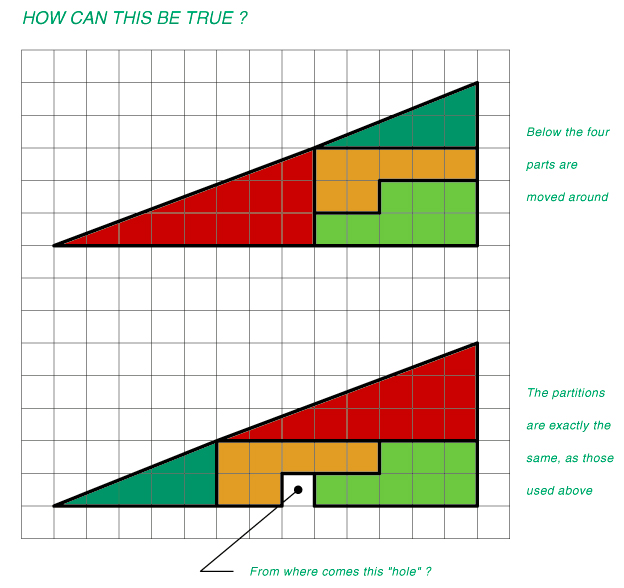
Ich habe das Bild sogar in Photoshop geöffnet und die einzelnen Bausteine ausgeschnitten, ob wirklich nachzuprüfen, ob alle Winkel und Kanten gleich sind.
Bevor ihr das Lineal rauskramt…. alles ist genau gleich.
Wer hat des Rätsels Lösung (vielleicht komm ich nicht drauf wegen der Riesenhitze >30° hier) ???
Schreibe einen Kommentar und die Welt wird weiser sein.
Lösung mathematisch angehen:
Dazu benötigen wir die Steigung einer Geraden (bitte in entsprechender Literatur nachsehen)
Steigung =m
m(grün)=2/5 = 0.4
m(rot) = 3/8 = 0.375
Damit es sich bei dem Bild oben um ein Dreieck handelt, müssten die Werte IDENTISCH sein, sind sie aber nicht. => Die Linie, die das große „Dreieck“ nach oben begrenz ist kein Dreieck, sondern ein 4 Eck, da es ja zwischen grün und rot nen Knick gibt. Der Unterschied ist sau gering, aber er reicht um ihn
1. optisch völlig zu übersehen und
2. den Flächeninhalt zu verfälschen.
Vielen Dank für die Antwort.
War ja dann doch igendwie klar, dass es sich nur um einen optischen Trick handeln kann, denn die Logik war ja eindeutig gebrochen!
Greetz
Bremmo
Lade das Bild mal in ein Grafikprogramm und zeih mit dem Linealwerkzeug ne Linie.. Du wirst sofort sehen, beide Dreiecke sind „gebeult“. Einmal nach innen, einmal nach aussen… 😉
Liebe Leutz,
das hier dargestellte Kuriosum hat mit den Kantenlaengen der Einzelteile und alternierenden Fibonacci-Zahlen zu tun.
Kein Lug kein Trug, keine optische Taeuschung 😉
Gruss,
strOEh
…ah ja.
Hier der Link fuer die Unglaeubigen und Wissbegierigen.
http://www.mcs.surrey.ac.uk/Personal/R.Knott/Fibonacci/fibpuzzles2.html
Viel Spass beim Klugscheissen.
strOEh
Hallo Steffen,
erstaunlich, dass Du Dich inzwischen für mathematische Probleme interessierst. Musste auch erst grübeln, war aber noch nicht so weit um zum Ausschneiden greifen zu müssen. Damit kann man das Problem auch nicht lösen, da mit bloßem Auge nicht zu erkennen ist, dass das rote und das grüne Teildreieieck nicht ähnlich sind. Dasselbe hat Dein erster Diskussionsteilnehmer (etwas anders) gesagt.
Grüße
Alois